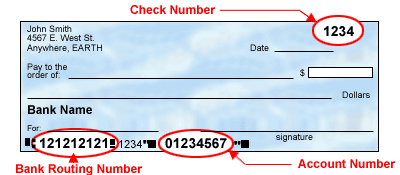
consultmili.blogg.se - Cc check digit

#Cc check digit how to
#Cc check digit full
#Cc check digit verification
#Cc check digit code

Such as credit card numbers, IMEI numbers, National Provider Identifier numbers in US and Canadian Social Insurance Numbers. The Luhn algorithm or Luhn formula, also known as the “modulus 10″ or “mod 10″ algorithm, is a simple checksum formula used to validate a variety of identification numbers, It is used to validate the credit card number using Luhn algorithm (Mod 10 algorithm). Last digit is known as check digits or checksum. Taking away the 6 identifier digits and the last digits, remaining digitsĪre the person’s account number (7th and following excluding last digits) It will identify the institution that issued the card. The first 6 digits are the Issuer Identification Number.

6 – Merchandising and Banking/Financial.

It designates the category of the entry which issued the card. The first digit of the credit card number is the Major Industry Identifier (MII). Typically, credit card numbers are all numeric and the length of the credit card number is between 12 digits to 19 digits.įor more information please refer.

#Cc check digit how to

Since the Luhn algorithm was initially developed to be calculated by a mechanical device, it can be compressed to as little as 1-2 lines in most modern programming languages.All you know what information contains in your NIC number. But do you know what information contains in the Credit Card Number?įollowing article provides brief details about what information contain in your credit card and demonstrates to how to validateĬredit card number using mod 10 (Luhn) algorithms with C#. This is highly recommended, as detecting a typo in a credit card number with a javaScript Luhn algorithm is much faster and more user-friendly than getting a rejected card error from your payment gateway.

#Cc check digit code

If you are a developer working with credit card numbers, you can use the Luhn formula to validate credit cards client-side or server-side using a variety of freely available code snippets and libraries. You can see the formula in action at our credit card validation tool, which uses the Luhn formula. However, the Luhn algorithm is more than powerful enough to catch most causual errors that will be encountered when working with credit card numbers. There are a few scenarios where invalid transpositions to a number would still be calculated as Luhn valid (such as transposing a "33" with a "66", etc). The Luhn algorithm is highly effective considering its simpleness, and is able to detect any single-digit errors and mst transpositions of adjascent digits. If the sum from step 2 modulo 10 is equal to 0 (e.g., if the total ends in zero) then the number is valid according to the Luhn formula.

After carrying out steps 1 (doubling every second digit from the right and subtracting 9 if result is > 9) and 2 (summing all digits, this time including the check digit), you can determine if the number is Luhn valid as follows: The process of verifying if a credit card number is valid according to the Luhn algorith is simple. Verifying a card number with a Luhn checksum

The units digit (3) is the check digit.

Compute the sum of the non-check digits (67).

For our example, the equation is 67 × 9 mod 10. The check digit can be obtained by computing the sum of the non-check digits then computing 9 times that value modulo 10. We still need to calculate the check digit, X. The sum of all the digits in the third row above is 67+x. In the following example, we use a sample credit card number "7992739871", with an unknown Luhn check digit at the end, displayed as 7992739871x:

Multiply the sum by 9, the Luhn check digit is the rightmost digit of the result (e.g, the result modulo 10).

Sum of all the digits in the newly calculated number.

From the rightmost digit (the check digit), move left and double the value of every second digit if doubled number is greater than 9 (e.g., 7 × 2 = 14), then subtract 9 from the product (e.g., 14: 14 - 9 = 5).

But first, we'll discuss how the Luhn check digit itself is calculated.

#Cc check digit verification

Therefore, when presented with any Luhn-verifiable account number, you can check for errors or transpositions by following the verification algorithm described below.

#Cc check digit full

The Luhn checksum works by calculating a check digit on the partial account number, which is then included as the last (rightmost) digit of the full account number. Invented in 1954 by an engineer at IBM, the Luhn algorithm has since been adopted as a standard by all major credit card issuers, as well as many government IDs, and is specified in ISO/IEC 7812-1. The Luhn algorithm is a simple, public domain checksum algorithm that can be used to validate a variety of identification numbers.